在本系列的前一篇文章中，我们介绍了缠结的数据结构。我们还了解tips，以及一个良好tip选择算法的重要性。今天，我们将学习交易速率和网络延迟，以及它们在确定缠结形态方面的作用。我们还将学习无权重的随机行走，此内容还将在下周进一步深入。

在上周的模拟中，你可能已经注意到，交易并不是随着时间均匀分布的，而是有些时段比其他时段“繁忙”。这种使得模型更加贴近现实的随机性，是通过使用泊松点流程来建模交易的到达方式。这种模型常见于分析在特定时间段内有多少客户进入商店或呼叫中心有多少个呼入电话。我们可以在下面的缠结例子中看到这个行为。交易4,5和6几乎同时到达，在交易6之后有一个较长的停顿。

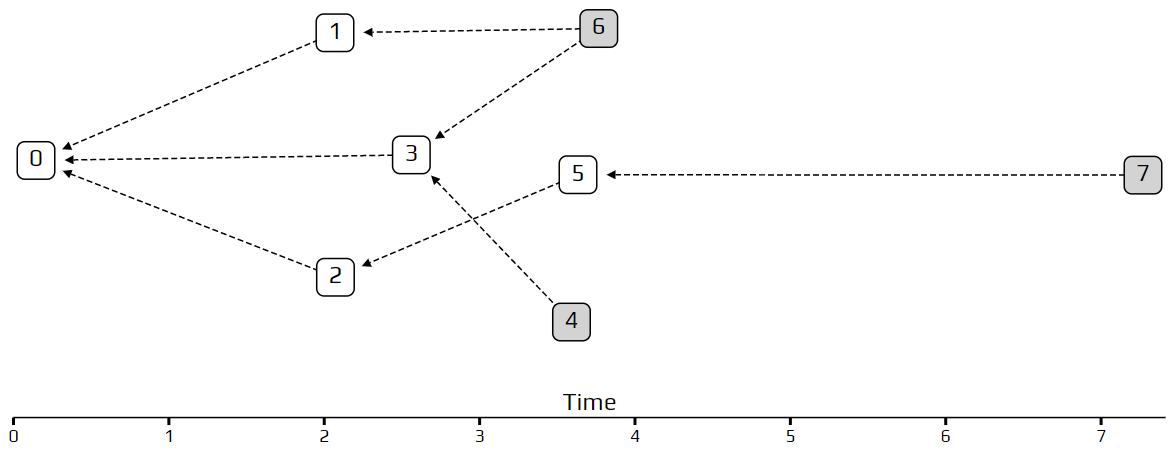
就我们的目的而言，我们只需要知道有关泊松点过程的一件事：平均而言，传入交易的速率是恒定的，并设为常数称λ。举一个例子，如果我们设置λ=2，和交易的数量是100，总的模拟时间将为大约50个时间单位。试一下！

更有趣的是，在继续之前：如果我们设置λ非常小，比如0.1，那我们将得到一个“链”。一个链也是缠结的，但交易事务只批准一个先前的交易，而不是两个。这是因为新增交易的速率非常低，抵至新交易只能选择一条以往交易来验证。在另一个极限情况下，设定λ的值非常大，所有的交易都快速出现，此情况下，所有tip都会看见初始交易。这只是在模拟状态下的限制性情况：大数值的λ和固定数量的交易事务，模拟发生在一个非常短的时间内。

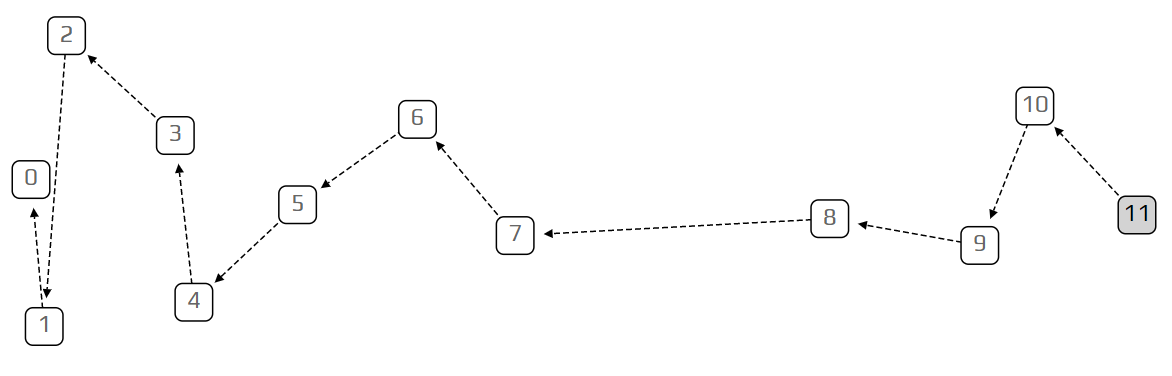
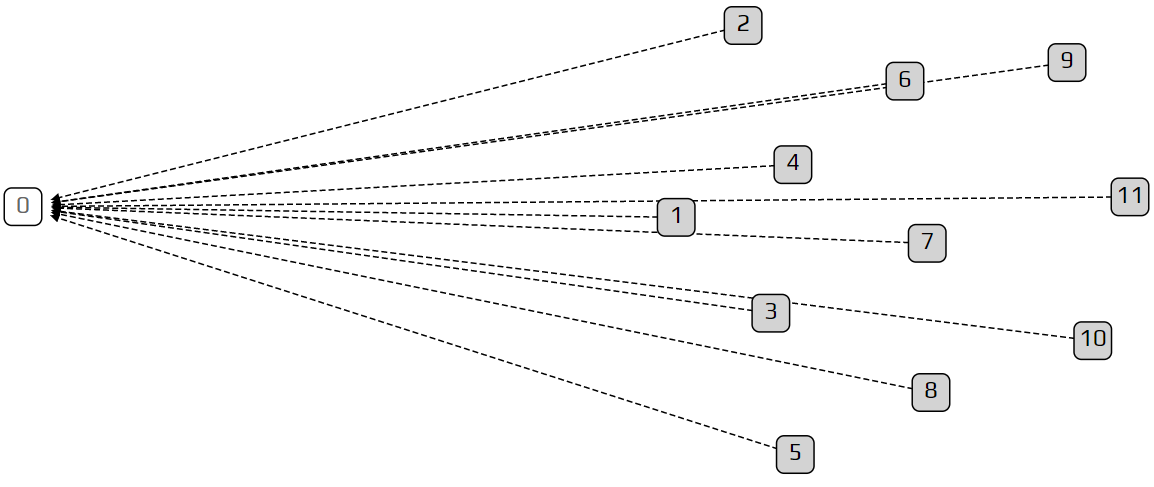
那么，看不见前面的交易是什么意思呢？在模型中，我们定义每笔交易在到达之后都会有一段时间不可见。我们用字母h标记这个延迟时间。这个延迟时间表示交易事务通过网络准备和传播所花费的时间。在我们的模拟中，我们总是设定h = 1。这意味着我们只能批准在过去至少有一个时间单位的交易。这种延迟不仅仅是为了增加模拟现实性的一个小细节，还是缠结的一个基本属性，没有它我们将永远只得到一个非常无趣的链条。它也使缠结更加接近现实世界，即人们总是需要一段时间来相互告知新的交易。

最后，就该说说一个更先进的tip选择算法：无权重的随机游走。使用这个算法，我们把一个行走者（比喻选择方式）置于起始交易上，让它开始走向tips。在每一步，相当于跳转到直接批准我们当前所在的一个交易。我们选择以相同的概率跳到某个交易，这就是无权重的随机行走。当然，我们已经做了一个模拟演示说明它如何发生。

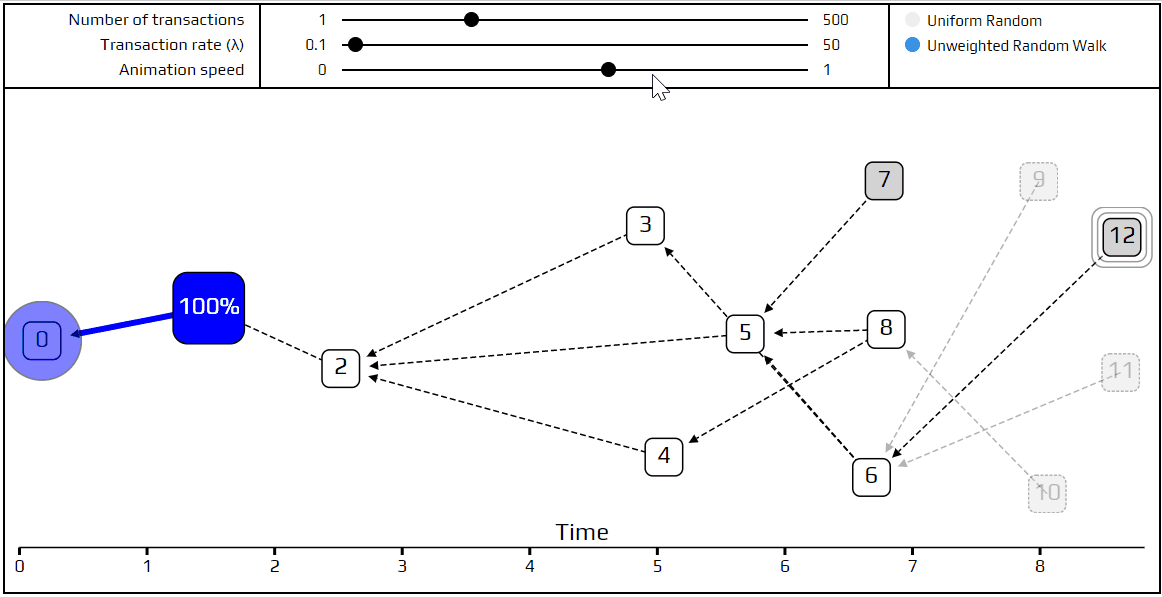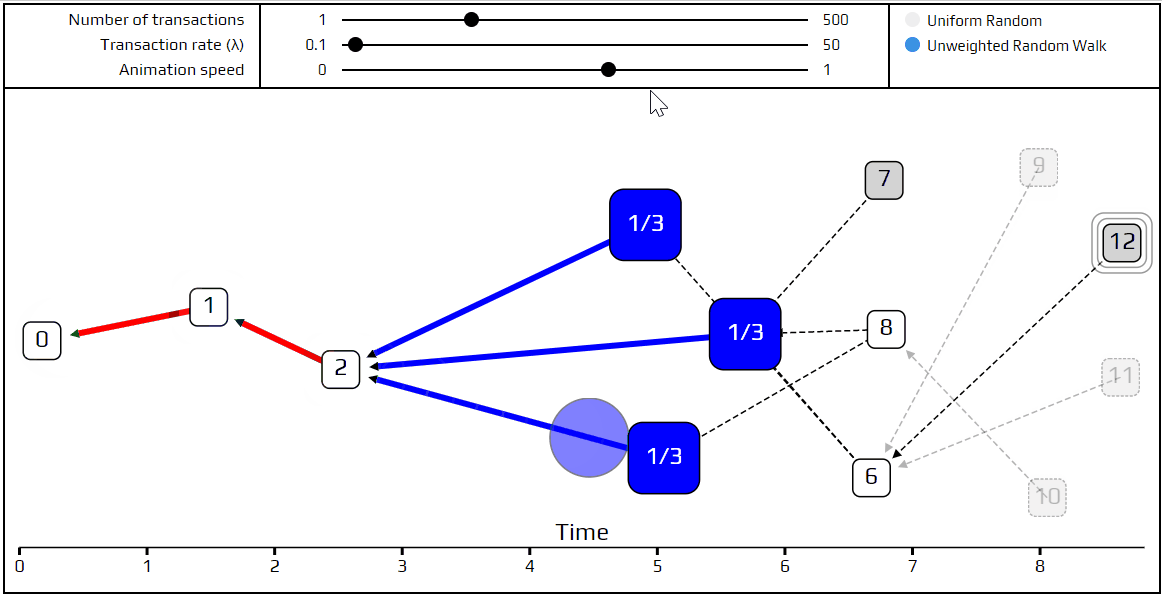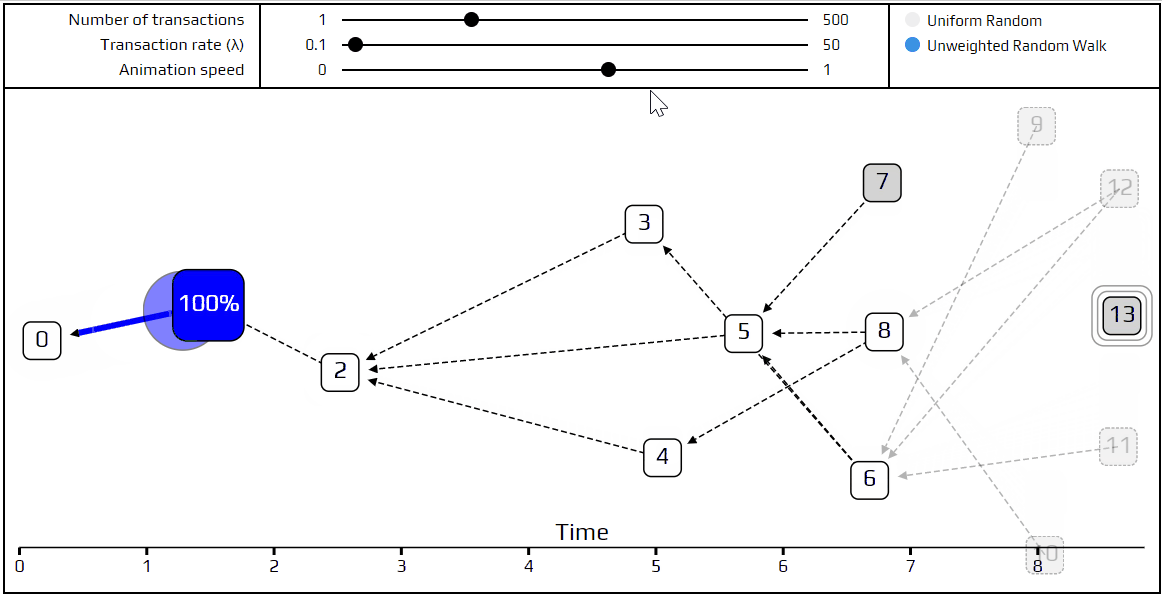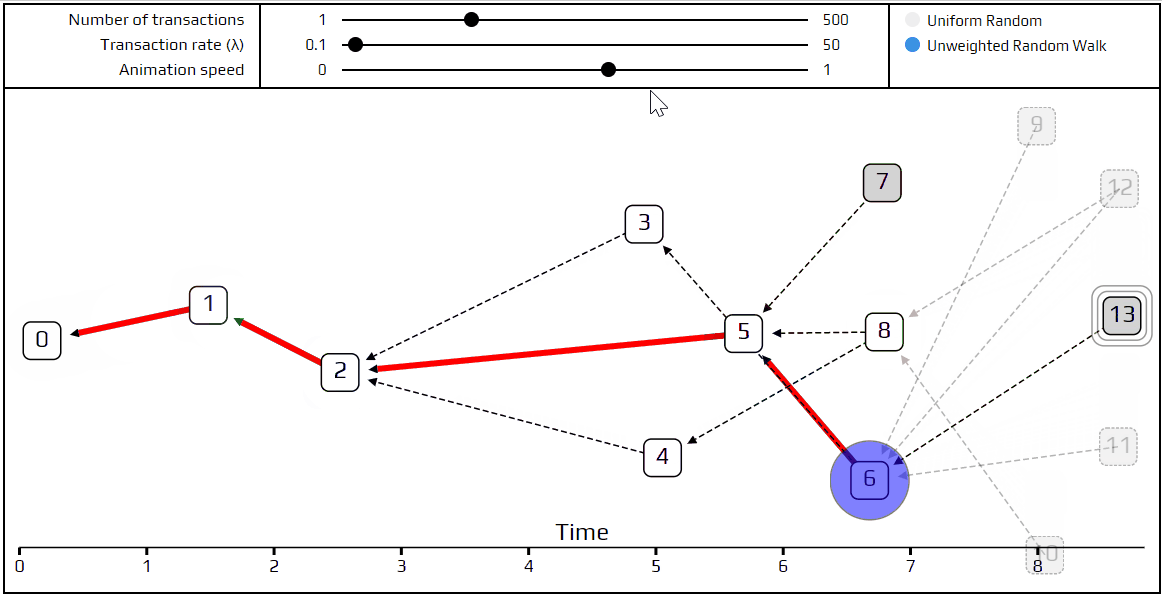
您可以看到“行走者”的路径标记为红色，并且在每个路口处，不同的可能选择的路径都标记为蓝色。非常短时间的交易对于当前的随机游走是“不可见的”，显示为透明。

我们今天的内容涵盖很多方面，所以请花时间认真阅读文章，在玩玩模拟游戏，并可以提出问题。欢迎您直接与我联系，在Discord上的alongal#3938是我的ID，或者在下面回复评论。下周，我们将学习累积权重，马尔可夫链蒙特卡罗和加权随机游走。

原文链接：https://blog.iota.org/the-tangle-an-illustrated-introduction-c0a86f994445