零数学基础理解MCMC（蒙特卡洛马尔科夫链）|IOTA中国社区 | IOTAChina

对于大多数人来说，贝叶斯统计方法简直就像巫语一样难懂或者是彻底的胡言论语。在众多贝叶斯实现方法中，马尔可夫链蒙特卡洛（MCMC）方法由于包含大量数学计算，显得尤其神秘。但他们背后的基本原理，就像数据科学中的其他东西一样，可以直观理解，也就是我的目标。

那么，什么是马尔可夫链蒙特卡罗（MCMC）方法？简单说就是：

MCMC方法用于通过在概率空间中随机采样来近似兴趣参数的后验分布。

在本文中，我将用非数学知识来简短回答。

首先，介绍一些术语。兴趣参数（parameter of interest）是我们感兴趣现象的一些数字。通常使用统计学评估参数。例如，如果我们想了解人类成年人的身高，我们的兴趣参数可能是精确到以英寸为单位的平均身高。分布是参数的每个可能值的数学表示，以及，我们有多大可能观察每个参数。最着名的例子是钟形曲线：

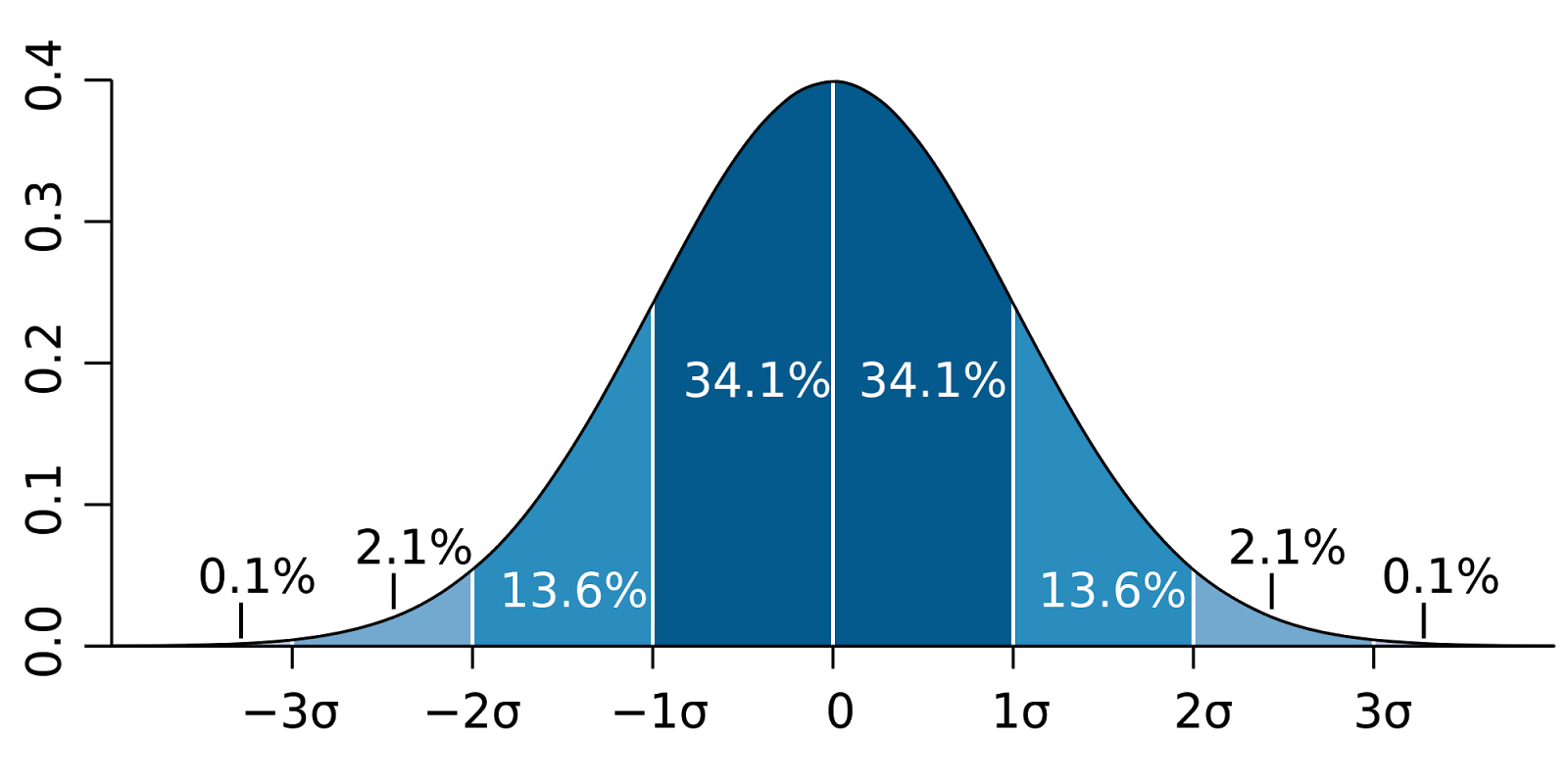
在贝叶斯统计方式中，分布有另外一种解释。贝叶斯不是仅仅代表参数的值以及每个参数为真的可能性有多高，贝叶斯认为分布描述了我们对参数的信念。因此，上面的钟形曲线表明我们非常确定参数的值接近于零，但是我们认为真实值高于或低于该值的可能性是相等的。

事实上，人的身高确实遵循正态分布曲线，所以我们假设我们认为的平均身高的真实值遵循如下的钟形曲线：

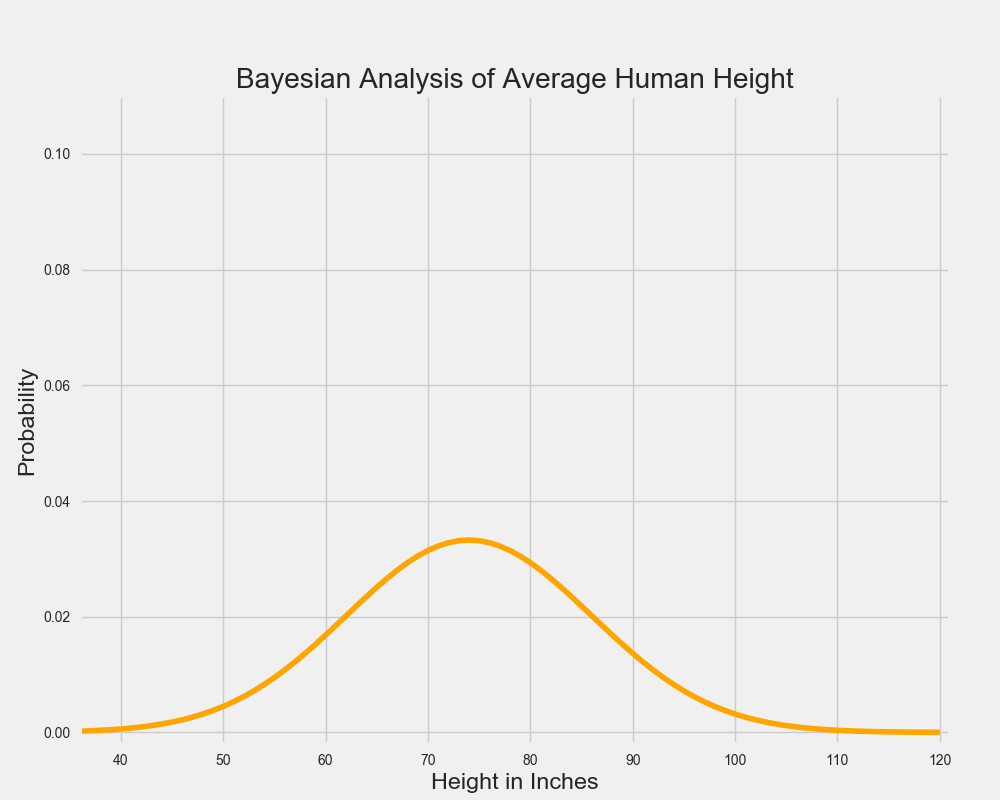
显然，这个图表所代表的信仰者已经生活在巨人之间多年，因为据此图所知，最有可能的平均成年身高是6'2“（但他们并不是超级自信）。

让我们假设这个信仰者收集了一些数据，他们观察到了一些身高在5”到6“之间的人。我们可以用下图来表示这些数据，表明哪个身高的平均值最能解释这些数据：

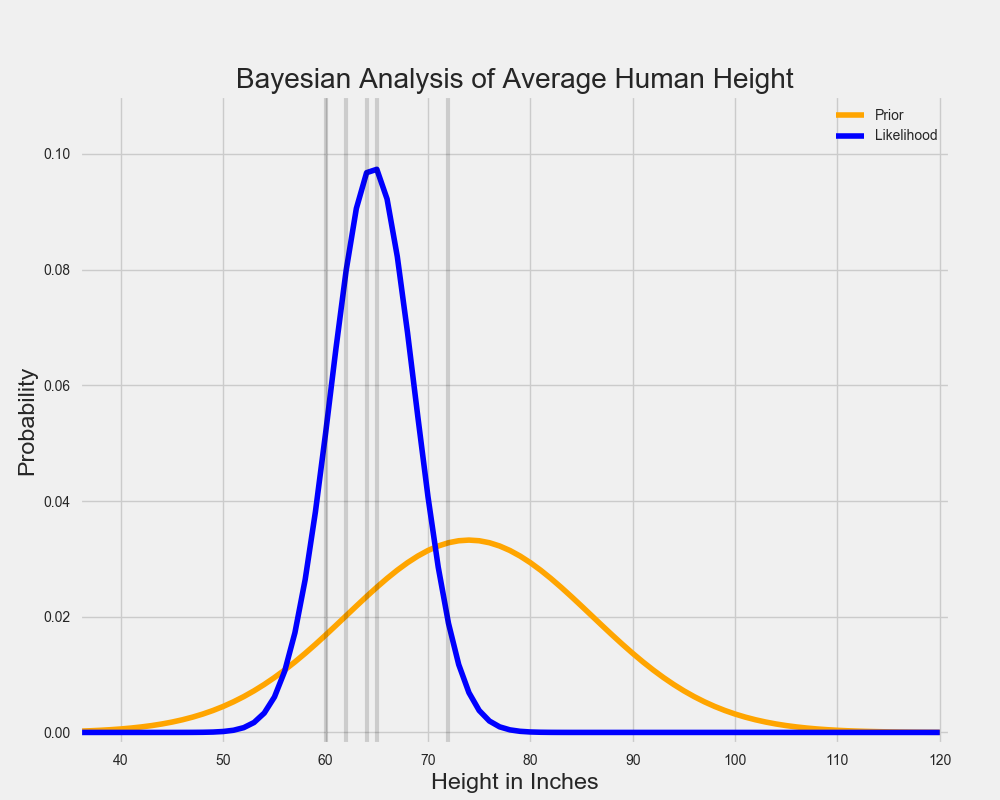
在贝叶斯统计中，代表我们关于参数的信念的分布被称为先验分布，因为它是在看到任何数据之前反映出的我们的信念。可能性分布概括了观察到的数据以及对应的参数值所观察数据的可能性。估算最大可能性分布的参数值只是回答了一个问题：什么参数值会使它最有可能反映出到我们观察到的数据？如果没有先验分布，我们可能就此止步。

然而，贝叶斯分析的关键是将先验分布和可能性分布结合起来确定后验分布。这告诉我们，考虑到我们先验分布状态，哪个参数值最大限度地反应出我们所做的特定数据。在我们的例子中，后验分布是这样的

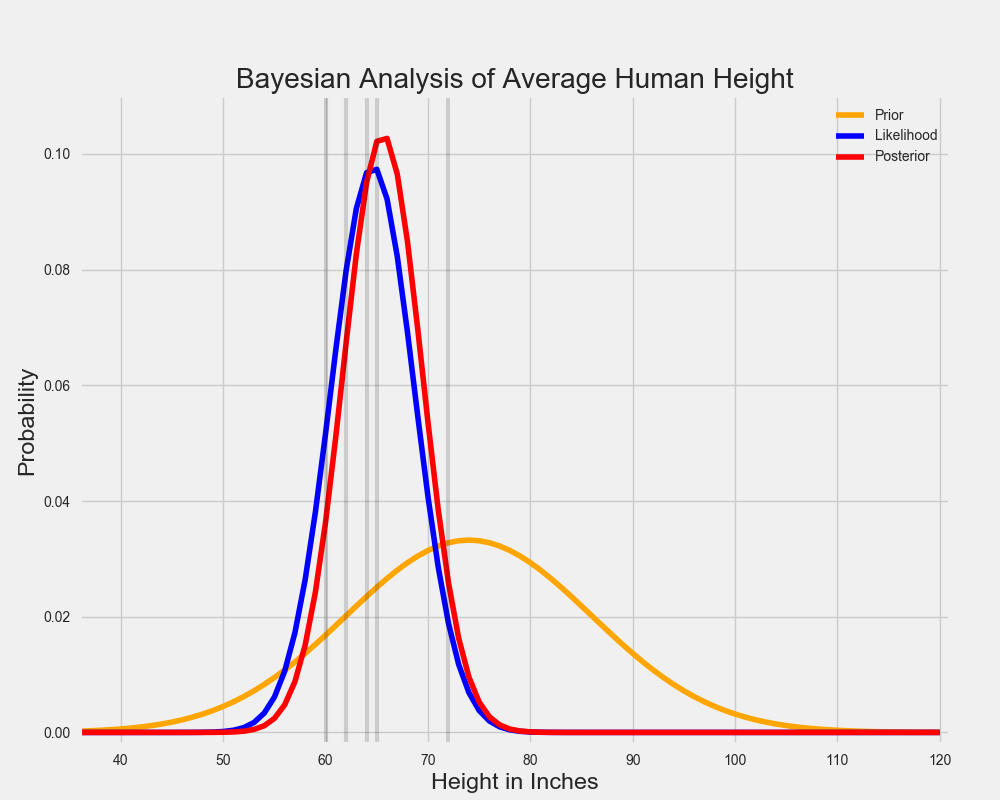
上面的红线代表后验分布。你可以把它看成是先验分布和可能性分布的平均值。由于先验分布数据少，分布更广，它代表一组”不确定“的平均身高真值的信念。与此同时，可能性分布会在一个相对较小的范围内对数据进行总结，因此它代表了对真值的“更确定”的猜测。

当先验分布和可能性分布被合并时，数据(由可能性分布表示)支配了假设存在于巨人中成长起来的个体微弱的先验信念。尽管该个体仍然相信人类的平均身高略高于数据值，但他可能会被数据说服。

在两个钟形曲线的情况下，求解后验分布非常简单。有一个简单的方程式把两者结合起来。但如果我们的先验分布和可能性分布表现不好呢？有时候，用那些非简化形状的分布来建模我们的数据或先验信念是最准确的。如果可能性分布最好由两个峰值的分布来表示时呢？由于某种原因，我们想要解释一些非常古怪的先验分布时呢？我已经想象了下面的场景，手工绘制了一个丑陋的先验分布:

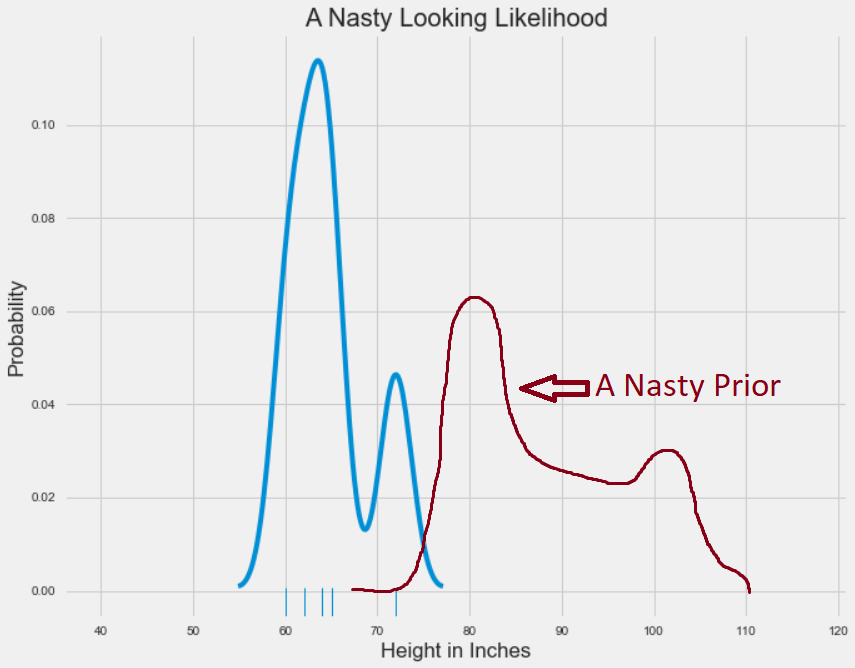
如前所述，存在一些后验分布，为每个参数值提供可能性分布。但是要想知道它看起来是什么样子有点难，而且不可能解析。这时MCMC该上场了。

MCMC方法允许我们直接评估后验分布的形状，而无需进行计算。为理解它工作原理，我首先介绍蒙特卡洛模拟，然后讨论马尔可夫链。

蒙特卡罗模拟只是一种通过重复生成随机数来估计一个固定参数的方法。通过生成随机数并对其进行计算，蒙特卡罗模拟提供了一个近似的参数，直接计算它是不可能或者计算量巨大。

假设我们想评估下圆的面积:

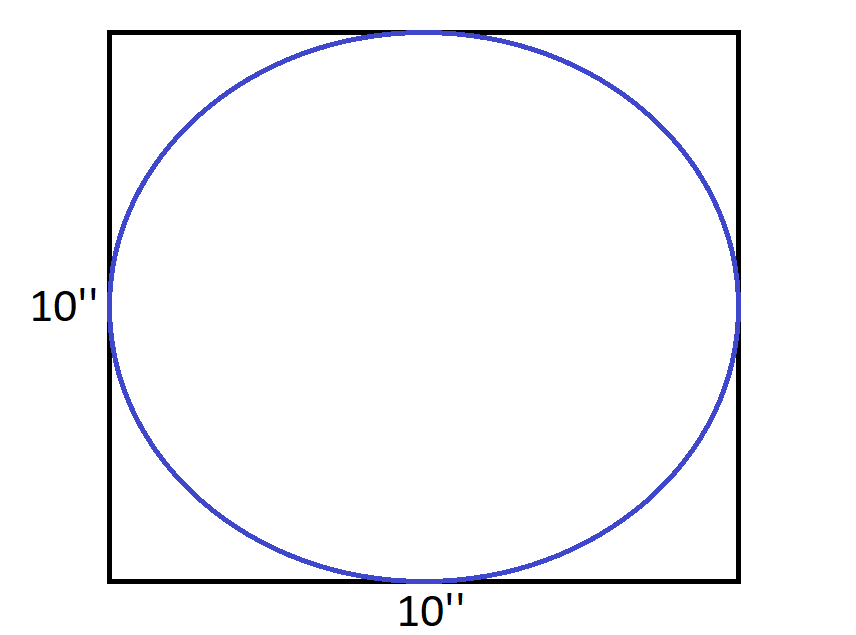
由于圆形所处的正方形边长为10英寸，所以面积可以很容易计算出78.5平方英寸。然而，我们可以在正方形内随机投掷20个点。然后我们计算在圆内的点的比例，然后乘以正方形的面积。这个数字将非常近似于圆的面积。

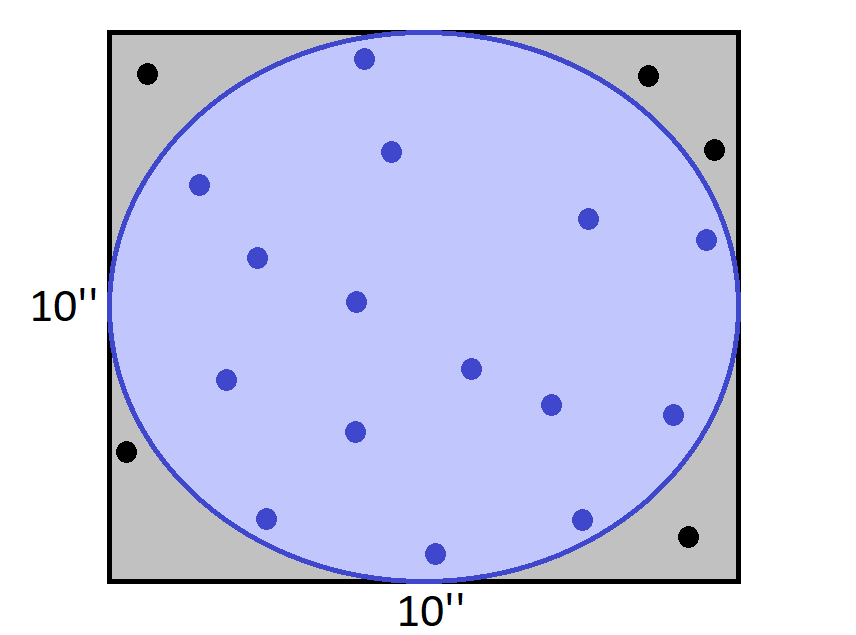
因为20个点中的15个都在圆圈内，所以看起来这个圆大约是75平方英寸。对于一个只有20个随机点的蒙特卡罗模拟来说，结果不算太坏。

现在，想象一下我们想要计算出蝙蝠侠方程形状的面积:

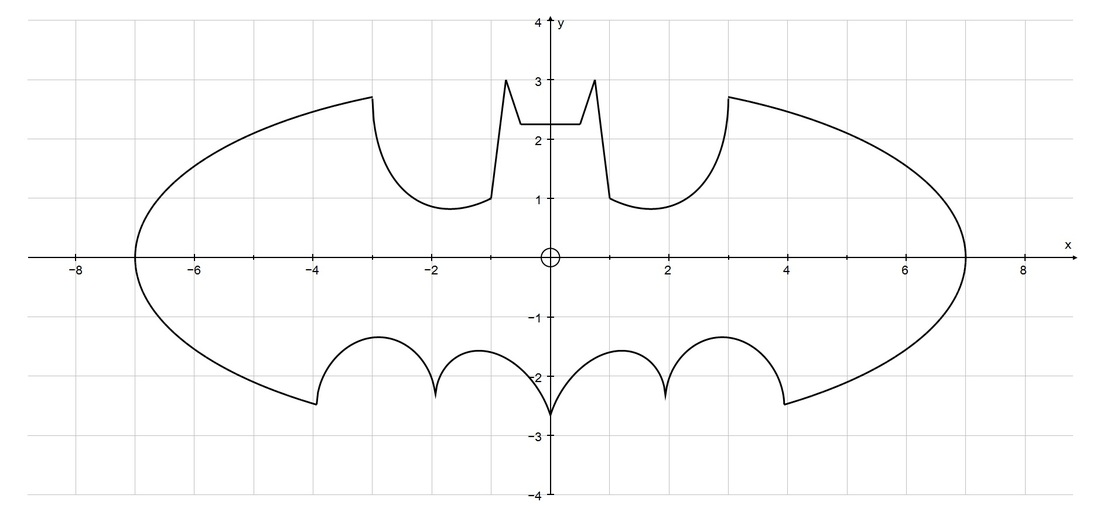
我们从未学过任何方法来求解这样形状的面积！但是，通过在包含随机形状的矩形内随机放置点，蒙特卡罗模拟可以很容易地提供该区域的近似值！

蒙特卡罗模拟不仅用于估计困难形状的面积。通过生成大量随机数，它还可以用对非常复杂的过程进行建模。在实践中，蒙特卡洛模拟被用来预测天气，或者估算赢得选举的可能性。

理解MCMC方法的第二个元素是马尔科夫链链。它是由简单的存在概率关联的事件序列构成。每个事件都来自一组结果，根据一组固定的概率，每一个结果决定了接下来发生的结果。

马尔科夫链的一个重要特征是它的无记忆性：可能需要预测下一个事件的所有因素在当前状态下是可用的，并且从事件历史中没有得到新的信息。像Chutes和Ladders这样的游戏展示了这种无记忆性，或者称为马尔科夫的特性，但现实世界中很少有东西是这样运作的。然而，即便如此，马尔可夫链仍然是理解世界的强大方式。

在19世纪，钟形曲线被认为是自然界的一种常见模式。(例如，我们注意到，人类身高遵循钟形曲线)，Galton board，通过将弹珠放入装有钉子的木板上，模拟重复随机事件的平均值，在弹珠分布上呈现出了钟形曲线:

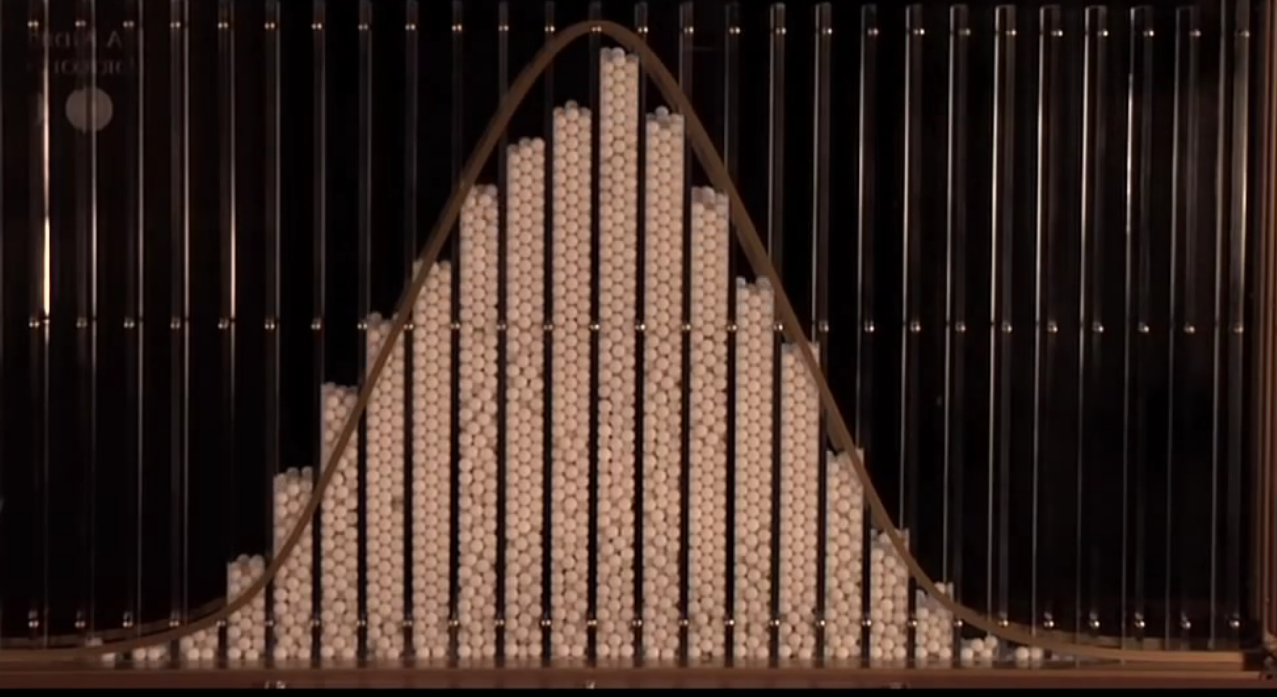
俄罗斯数学家和神学家Pavel Nekrasov认为，钟形曲线，或者一般称为，大数定律，只不过是儿童游戏的产物，每个事件都是完全独立的。他认为，现实世界中的事件都是相互依赖的，如人类行为，并不符合良好的数学模型或分布。

Andrey Markov，试图证明非独立事件也可能遵循某种模式。他最著名的例子之一就是要数出俄罗斯诗歌作品中成千上万的两对字符。使用这些两对字符，他计算了每个字符的条件概率。也就是说，给定前一个字母或空格，下一个字母可能是a, T，或空格。利用这些概率，Markov能够模拟任意长的字符序列。这就是马尔可夫链。虽然最初的几个字符很大程度上是由初始字符的选择而决定的，但Markov指出，从长远来看，字符的分布形成了一个特定模式。因此，即使是相互依赖的事件，如果它们服从于固定的概率，也要遵循平均值。

举一个更有用的例子，想象你住在一个有五个房间的房子里。你有一间卧室、一间浴室、一间客厅、一间餐厅和一间厨房。然后我们收集一些数据，假设知道你当前所处房间和时间就能预测下一个你所处的房间的概率。举例来说，如果你是在厨房里，你有30%的机会待在厨房里，有30%的几率进入餐厅，20%的机会到客厅里去，10%的几率进入浴室，和10%的机会进入卧室。利用每一个房间的概率，我们可以构建一个预测链，评估你可能出现的下一个房间。

如果我们想预测某人在离开厨房后所处的房间，假设几个状态而做出的预测则可能是有用的。但是因为我们的预测只是基于一个人在房子里的观察，所以认为预测结果不会很好则是合理的。例如，如果有人从卧室走到浴室，相比从厨房走到浴室，他们更可能直接回到卧室。所以马尔可夫特性通常不适用于现实世界。

然而，运行马尔可夫链进行数千次迭代，确实可以对您可能进入的房间进行长期预测。更重要的是，这个预测并没有受到这个人从哪个房间开始的影响！从直觉上讲，这是有道理的：时间因素对于模拟和描述某人在家中可能在长期或总体上的位置概率并不重要。所以马可夫链不是在几个周期内建模一个随机变量的合理方法，但如果我们理解控制其行为的概率，就可以用来计算这个变量的长期趋势。

我希望通过介绍一些蒙特卡洛模拟和马尔科夫链的知识，可以使零数学基础的人更好理解MCMC的方法。

让我们回到原来的问题，即评估平均身高的后验分布：

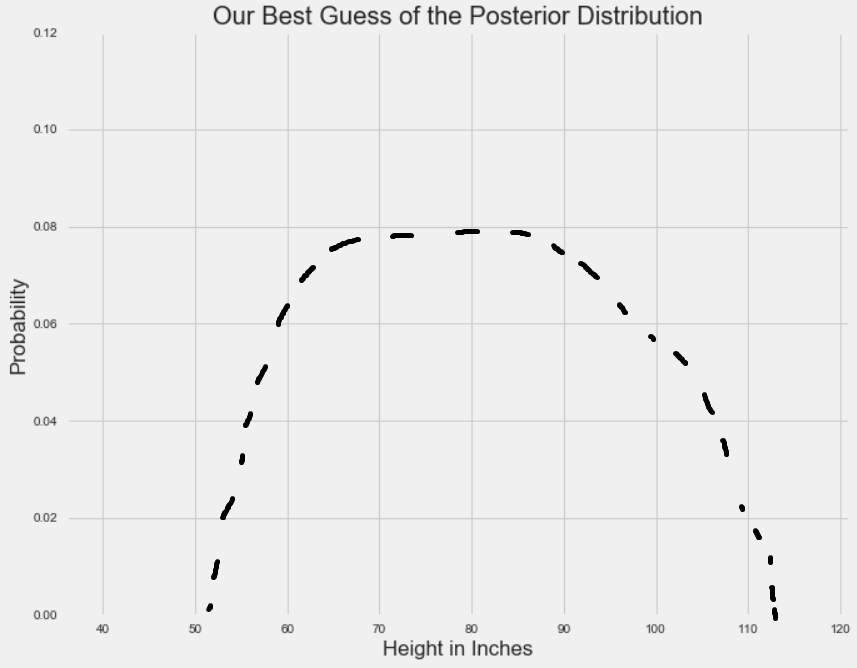
*我不是一个可视化的专家，我也没有把这个例子放在常识的范围之内：请不要在意我的后验分布例子严重高估了人的平均身高，这一小问题。*

我们知道某种程度上后验分布是在先验分布和可能性分布范围内的，但无论怎样，我们都无法直接计算它。利用MCMC方法，我们可以有效地从后验分布中抽取样本，然后计算出样本的均值。

首先，MCMC方法选择一个随机参数值来考虑。模拟过程将继续生成随机值(这是蒙特卡罗部分)，但是要遵循一些规则来确定什么是好的参数值。关键在于，对于一对参数值，可以通过计算每个值对数据进行解释的可靠性来计算，从而确定更好的参数值。如果一个随机生成的参数值比上一个参数值好，那么它就会被添加到参数值链中，出现参数值好的概率取决于它最后结果的优劣(这是马尔科夫链部分)。

为了直观地解释这一点，让我们回想一下，在某个值上分布的高度代表了观察到这个值的概率。因此，X轴（参数）对应的Y轴（概率）的值可高可低。对于单个参数，MCMC方法会首先在X轴上随机取样:

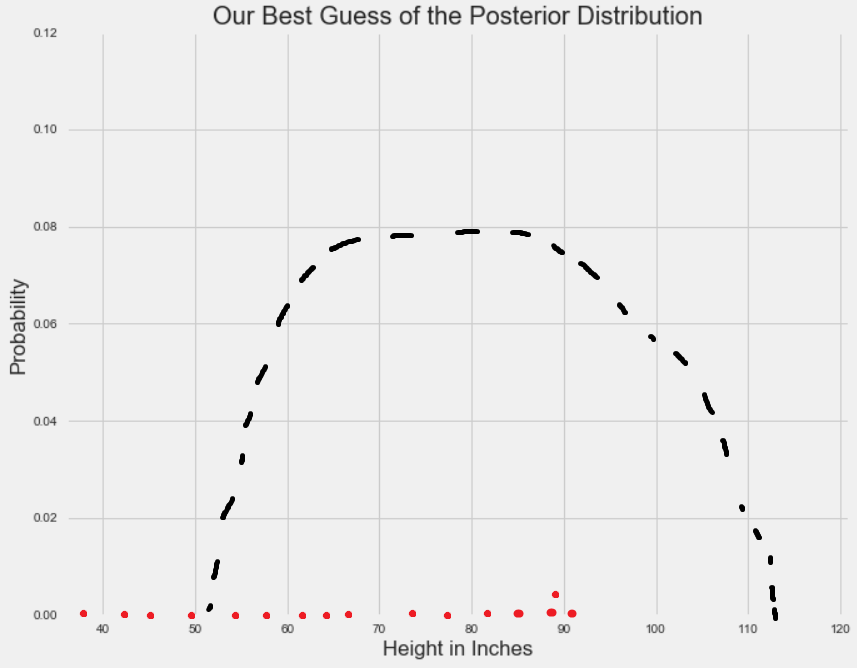
由于随机样本的概率是固定的，所以在我们感兴趣参数的最高概率区域中，它们趋向于收敛。

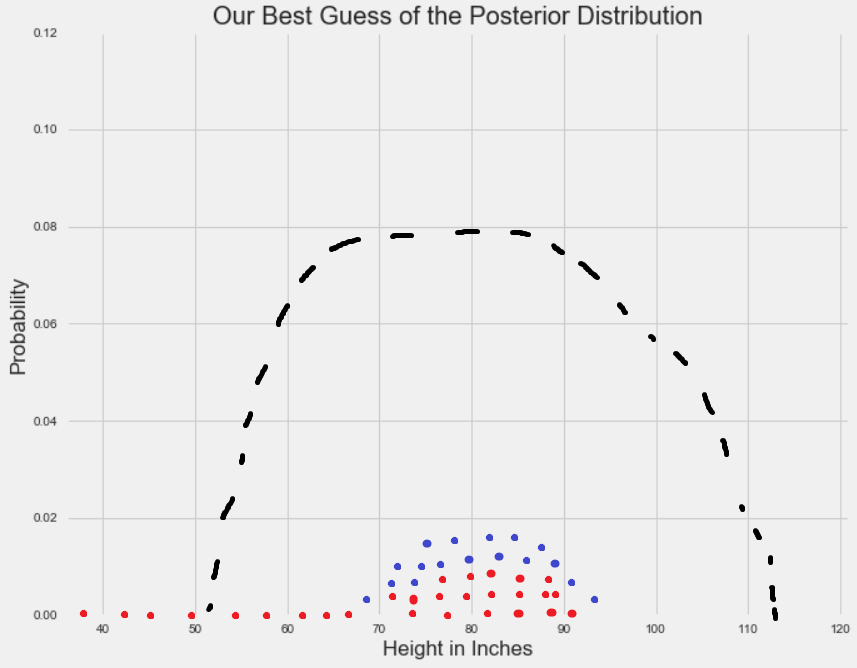
蓝点只代表采样收敛后，在任意时间点之后的随机样本。注意：为了说明的目的，我是垂直叠加的。

在收敛发生之后，MCMC采样区间产生一组来自后验分布的样本点。在这些点周围绘制直方图，并计算您喜欢的任何统计数据：

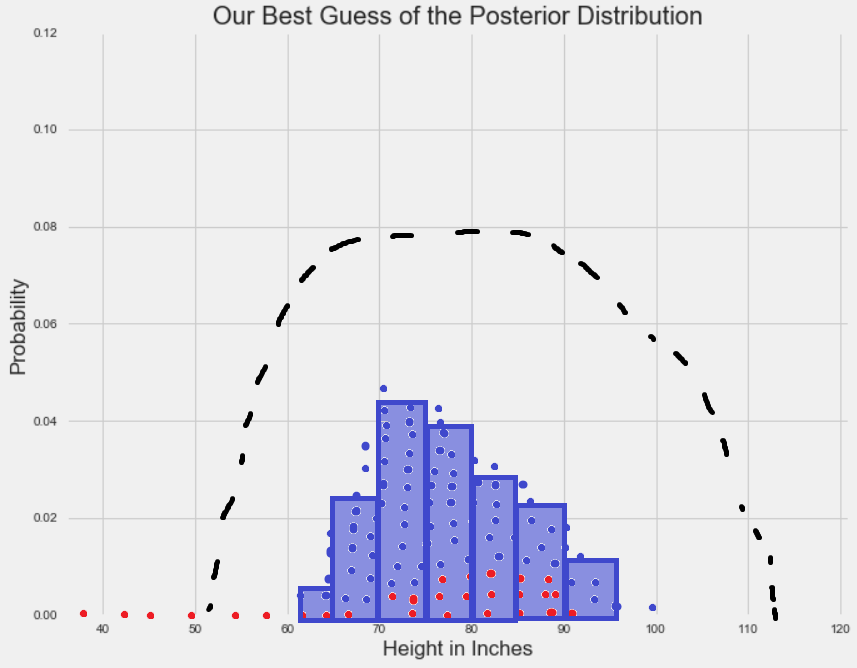
根据MCMC方法模拟生成的样本集计算出的任何统计数据分布特征，都是我们最可能接近真实后验分布统计量的结果。

MCMC方法也可以用来评估多个参数的后验分布（比如说人的身高和体重）。对于n个参数，在n维空间中存在高概率的区域，其中某些参数值组合更好地解释观察到的数据。因此，我认为MCMC方法本质就是在概率空间内随机采样以近似后验分布。

回想一下“什么是马尔可夫链蒙特卡罗方法？”这个问题的简短答案。

MCMC方法用于通过在概率空间中的随机采样来近似出兴趣参数的后验分布。

我希望我已经解释的简短答案，能让你理解为什么要使用MCMC方法，以及它们是如何工作的。这篇文章的灵感来源于我在华盛顿特区举行的Data Science Immersive课程。这个演讲的目的是向非技术观众解释马尔可夫链蒙特卡洛方法，我也试图通过此文完成同样的目标。如果您认为这个解释不符合标准，或者可以更直观一些，欢迎留下评论。

原文链接：https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50

喜欢 (19)